- 時系列分析に興味がありチャレンジしてみたい方
- 時系列モデルの基本的な使い方を知りたい方
- Pythonでこれからも分析をしていきたいという方
ご訪問いただきありがとうございます。本記事ではPythonを使った基本的な時系列データの分析や予測を実際のデータを使っての実践を通して、時系列データの基本的な扱い方、分析手法について解説していきます。時系列分析に興味がある方の最初の一歩としてお役に立てられれば幸いです。
実際の東京の2012年~2021年までの約10年間の平均気温データで、代表的な時系列分析手法で予測性能を比較してみました。それぞれのモデルではどのような違いが出るのでしょうか?さっそくみていきましょう。
なお、Pythonを中高年が基礎から最速独学で学ぶ方法を別の記事でまとめていますので、よろしければご覧ください。>> 中高年の為の挫折しない最短のPython,AI・機械学習のおすすめ学習方法
>> 中高年がAI・機械学習を学ぶ為のプログラミングスクール 主要8校を徹底比較
代表的な時系列モデルは何があるの?
時系列分析の代表的なモデルとしては、統計的な手法として広く認知されているものである手法にAR,ARMA,SARIMAなどがあります。さらに2016年ごろにFacebookのエンジニアが開発したProphetがあります。
- AR :自己回帰モデル ( Auto Regression )
自らの過去のデータから、未来のデータを回帰によって導きます。失業率や株価の分析などに使われています。 - ARMA: 自己回帰移動平均モデル ( AutoRegressive Moving Average )
AR(自己回帰)とMA(移動平均)を組合わせたモデル - SARIMA: 季節自己回帰和分移動平均モデル ( Seasonal AutoRegressive Integrated Moving Average )
ARIMAにSeasonal(季節性の周期)を加えたモデル - Prophet
Facebookが開発したオープンソースソフトウェア。 年、週、の周期性や休日などの影響も加えることが出来る
モデル比較の方法
- 気温データの取得
2012年~2021年8月までの東京の平均気温を入手(気象庁のデータから入手します) - データの分割
学習データ:2012年~2018年
テストデータ:2019年~2021年8月
簡易的な比較とするために、月平均データとする - モデルで予測
PythonでAR, ARMA, ARIMA, SARIMA, Prophetの5つのモデルで予測、検証する - モデルの比較、検証
2019年~2021年8月までの予測値と実測値のかい離率であるMAPEで評価
1.気温データの取得方法
今回は、モデルの比較検証を行うことを目的にするので、周期性のわかりやすい外気温のデータを使ってすすめたいと思います。データソースは気象庁から東京の2012年~2021年までの約10年間のデータを入手しています。ご興味がございましたら気象庁データから任意の場所、期間でデータを入手してみてはいかがでしょうか。
入手したCSVデータをPythonで読み込みます。
#csv読み込み
df = pd.read_csv("気象データ10.csv",index_col=0, encoding = 'shift-jis',parse_dates=True)
print(df.shape)
df.head(5)入手したデータを確認すると、平均気温、降水量、日照時間が入っています。(これ以外にも風速や積雪情報なども入手できますよ)データ数は、3507行、3列のデータとなっています。
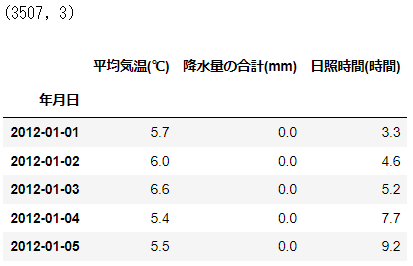
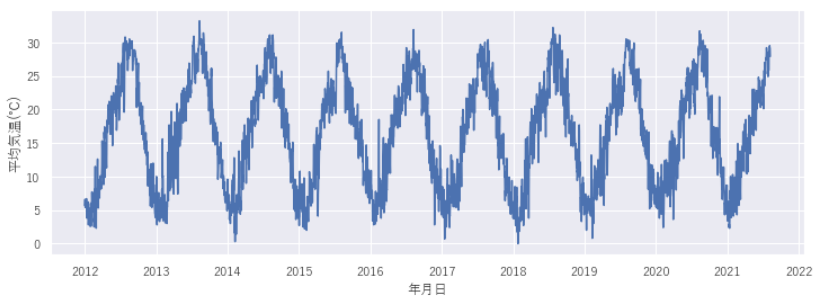
2012年~2021年8月までの東京の平均気温データ(日別)を入手します。線グラフであらわすと、以下のような時系列データになります。春夏秋冬の気温の変化が見て取れます。
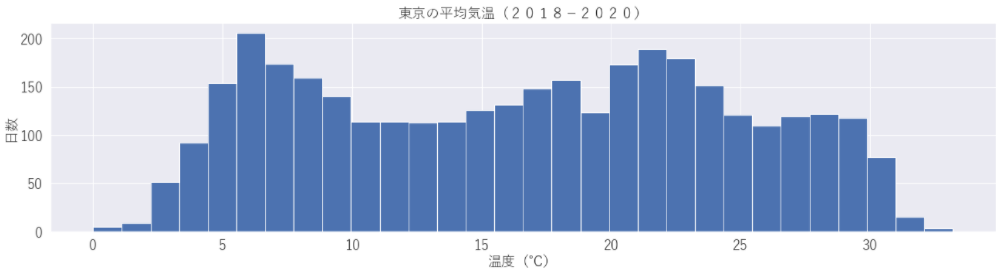
2018年~2020年までの気温をヒストグラムであらわすと下図のようになります。年間を通して6~7℃の日が多いんですね。感覚的には15~20℃程度の日が多いのかなと感じていましたが意外な結果ですね。
コレログラムとは
続いて、コレログラムをみていきましょう。コレログラムって??
コレログラムとは、日本語では自己相関図といいます。言葉のとおり自分のデータが時系列でみたときに相関がありますか、ありませんかということがわかるものです。
下のグラフでは、x軸が期間、y軸に相関係数をあらわしています。下のグラフでは、1年間(365日)を通して、周期的な波形があらわれています。x軸が0の部分がそもそも自分なので相関係数は1となり、そこからx軸の350から400付近をみると、y軸は同様に0.75~0.8の相関があります。つまり1年後の結果と1年前の結果は、強い相関関係があるといえます。今回の例では、外気温なので例年の季節的な気温は当然、大きく変わらないので強い相関があるのは当然の結果です。
それでは、どんなときにコレログラムを使うのでしょうか?そうですね、今回の例ではコレログラムを書かなくてもこのように、周期性があるということはわかりますが未知のデータでさらにデータのばらつきが大きい場合に、時系列データをみただけでは周期性があるかどうかは判断が困難です。そんなときにコレログラムでみてあげると、客観的に周期性の相関がみえてきます。相関関係があれば、未来の予測に対する示唆のひとつになるわけです。
import statsmodels.api as sm
plt.rc("figure", figsize = (12,6))
corr = sm.graphics.tsa.plot_acf(df["平均気温(℃)"],lags = 1000)
# x 軸がどの程度ずらしているかをあらわし、y軸に相関の強さを表している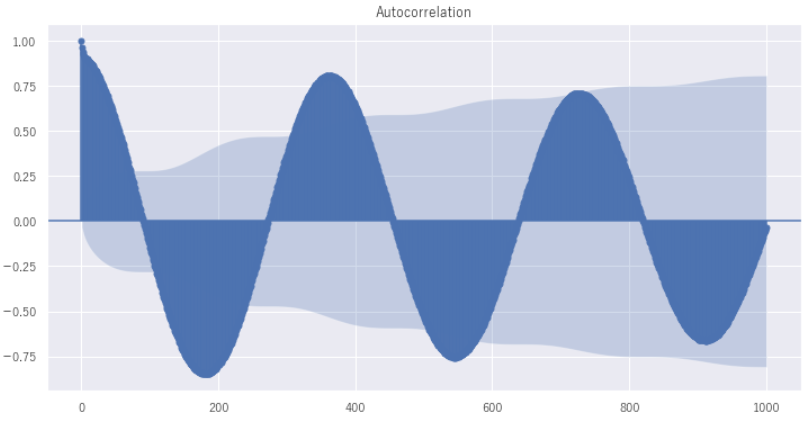
波形分析とは
続いて波形分析をみていきます。ここもさきほどのコレログラム同様、データの性質、傾向をみるいわばEDA(探索的データ分析)のひとつといえます。下記のコード1行で波形分析に必要な4つのグラフを生成してくれます。めっちゃ便利ですね。
では、グラフからみてとれることは何でしょうか。
Observedでは、時系列データの線グラフをあらわしています。全体感をみることと、その下にあるグラフとの関係性をみるときにも役に立ちます。
Trendでは、周期性をいったん外してみてみたグラフになります。周期性をいったん外すとどんないいことがあるかというと、周期的な動きに惑わされずにデータの変化に気づくことができることです。つまり今回の例では、x軸が500付近(おおよそ2013年の夏)、2400付近(おおよそ2018年の夏)では上昇しています。ということは2013年、2018年の夏は普段の夏と比べて暑かったと判断ができるのです。
Seasonalでは、逆に周期性を際立たせたグラフになっています。こうすることでどのようなパターンの周期となっているかが明確になってきます。
Residualでは、上記のTrendやSeasonalから排除されたいわばノイズです。逆にここに周期性やトレンドのようなパターンがあるとそれは何か間違っている可能性があるともいえます。
wave = sm.tsa.seasonal_decompose(df["平均気温(℃)"].values, freq = 365).plot()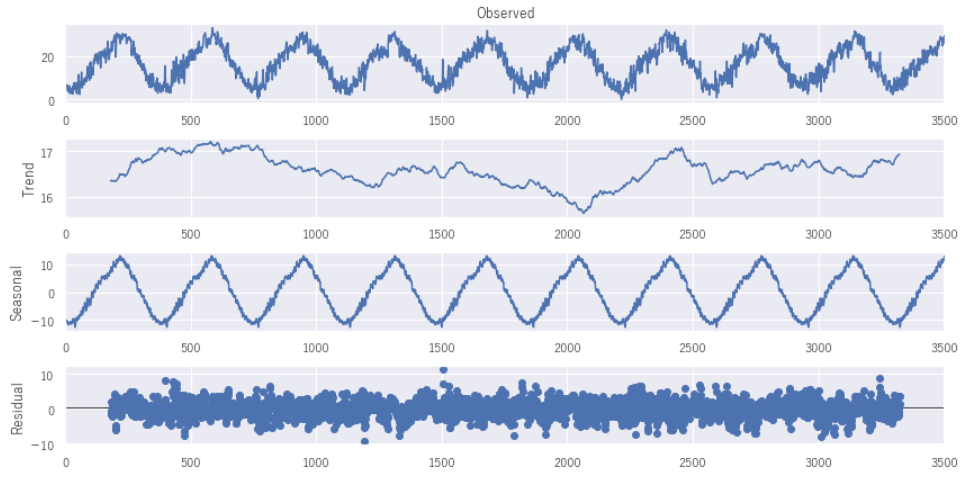
2.データの分割方法
それぞれのモデルで予測と検証を行うため、同じ条件で予測さる必要があります。そのためデータを学習データとテストデータに分割しておきます。
学習データ:2012年~2018年 東京の平均気温
テストデータ:2019年~2021年8月 東京の平均気温
また簡易的な比較とするために、月平均データとします 。月平均データにしてグラフをみてみるとギザギザがなくなり、より周期性が読み取りやすいデータになっていますね。データフレームでtrainには学習データを格納し、testにはテストデータを格納しています。
# 月ごとに集計したデータも準備しておく
df_month = df["2011":"2021"].resample("M").mean()
train = df_month["2012":"2018"]["平均気温(℃)"]
test = df_month["2019":"2021"]["平均気温(℃)"]
sns.lineplot(data = df["平均気温(℃)"].resample("M").mean())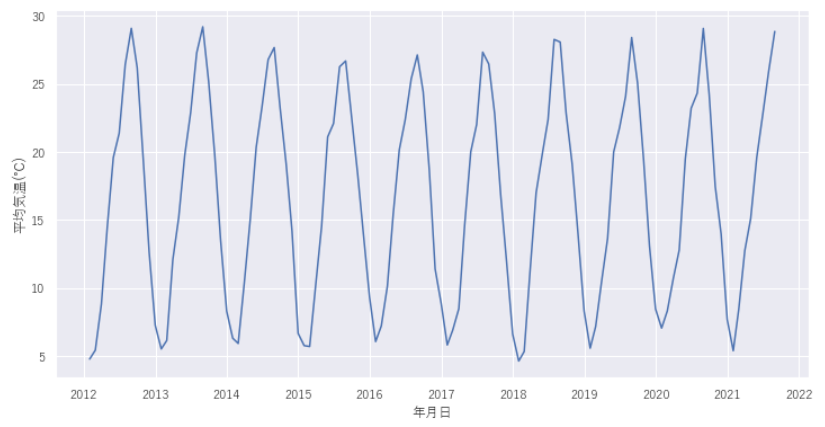
3.モデルを使って予測する方法
それぞれのモデルで平均気温データを用いて学習、予測を実行します。
最初に必要なライブラリをインポートしておきます。
Prophetのインストールについては次のブログ記事を参考にしてみてください。
# 必要なライブラリのインポート
from statsmodels.tsa import stattools as st
from statsmodels.tsa.ar_model import AR
from statsmodels.tsa.arima_model import ARMA,ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
# Prophetを利用した予測
from fbprophet import Prophet
from fbprophet.plot import add_changepoints_to_plot
# 基本的なライブラリ
import pandas as pd
pd.options.display.max_columns = None
pd.options.display.max_rows = None
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
sns.set()
sns.set(font=["Yu Gothic", "Hiragino Maru Gothic Pro"])
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
from sklearn.model_selection import train_test_split
from dateutil.relativedelta import relativedeltaARの予測結果
モデルの定義~予測
予測のコードはたったこれだけ、簡単ですね~。モデルの定義を行い、.fit()で学習し、期間を指定して予測しています。predict(start=len(train), end=len(df_month))では、学習データの最後の行~dfの最後の行。つまりテストデータをあらわしています。
# モデルの定義
model_ar = AR(train)
# モデルの学習
result_ar = model_ar.fit()
# 予測
prediction_ar = result_ar.predict(start=len(train), end=len(df_month))可視化
予測した結果をグラフ化してみましょう。グラフをみるとオレンジが予測線で青線が実績線です。最高気温は、かい離が大きそうですが周期的な温度変化はきちんと捉えていそうです。
# AR 月平均
plt.plot(test,label="data_test")
plt.plot(prediction_ar,label = "ar")
#以下表示設定
plt.title("2019-2021-9平均気温 実績と予測 @東京", fontsize=18)
plt.xlabel("", fontsize=18)
plt.ylabel("温度(℃)", fontsize=18)
plt.subplots_adjust(bottom = 0.3)
plt.tick_params(labelsize=18) # x,y軸の目りフォントサイズ
plt.legend(bbox_to_anchor=(0.01, 1), loc='upper left', borderaxespad=0, fontsize=18)
plt.subplots_adjust(left = 0.1, right = 0.8)
# グラフにきちんとおさまるようにする
plt.tight_layout()
plt.show()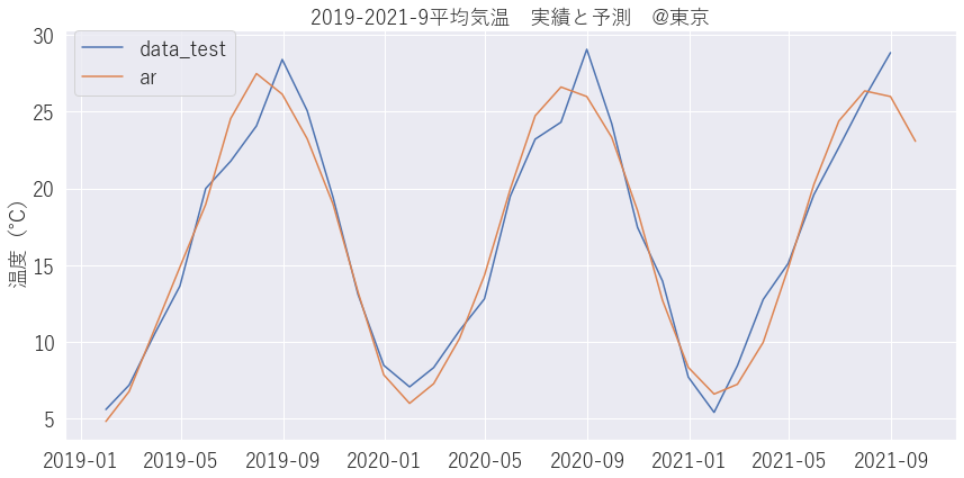
ARMAの予測結果
つづいてARMAモデルで学習、予測をしてみましょう。
やり方はARとほとんど一緒ですが、ARMAでは、パラメータである次数を指定する必要があります。ARの次数p は自己回帰部分の次数、MRの次数q は移動平均部分の次数をあらわし、下記コードでは[1,1]としていますが左がAR、右がMRをあらわしています。最初は最適な次数がわからなのでとりあえず[1,1]で学習、予測してみます。
# ARMA p,q 調整前(月平均) 予測
model_arma_b = ARMA(train, order = [1,1])
result_arma_b = model_arma_b.fit()
prediction_arma_b = result_arma_b.predict(start=len(train), end=len(df_month))うまく予測出来ていませんね。パラメータを調整してみましょう。
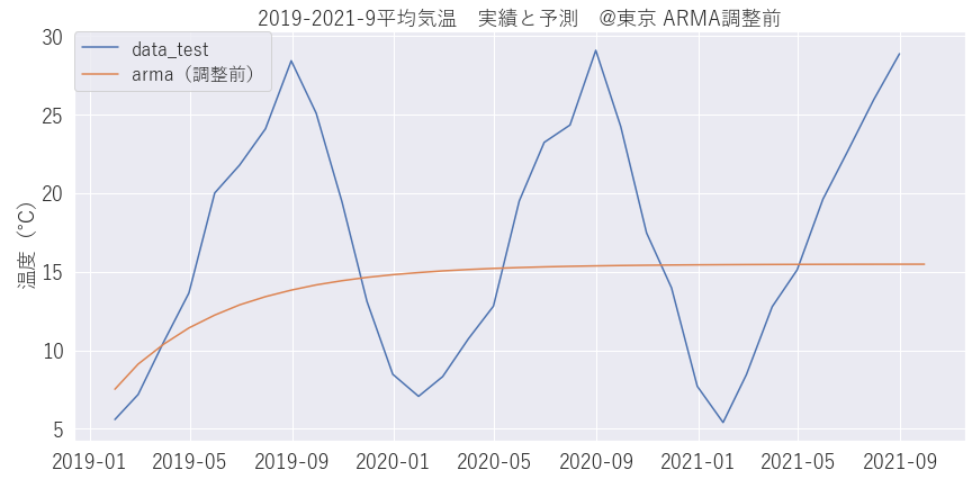
ARMA パラメータの調整
最適なパラメータを見つける為にstats modelのarma_select_icを使い、パラメータを総当たりさせて最適なパラメータを設定します。max_ar、max_maで総当たりする数を決めます。パラメータ設定の指標には赤池情報量基準(Akaike Infomation criterion, AIC)を用います。数値が小さいほど当てはまりがよくなります。
from statsmodels.tsa.stattools import arma_order_select_ic
arma_order_select_ic(train, max_ar=4, max_ma=7, ic="aic")下表が出力され、aic_min_orderが4,2となっています。表の4行2列が最小の値となります。

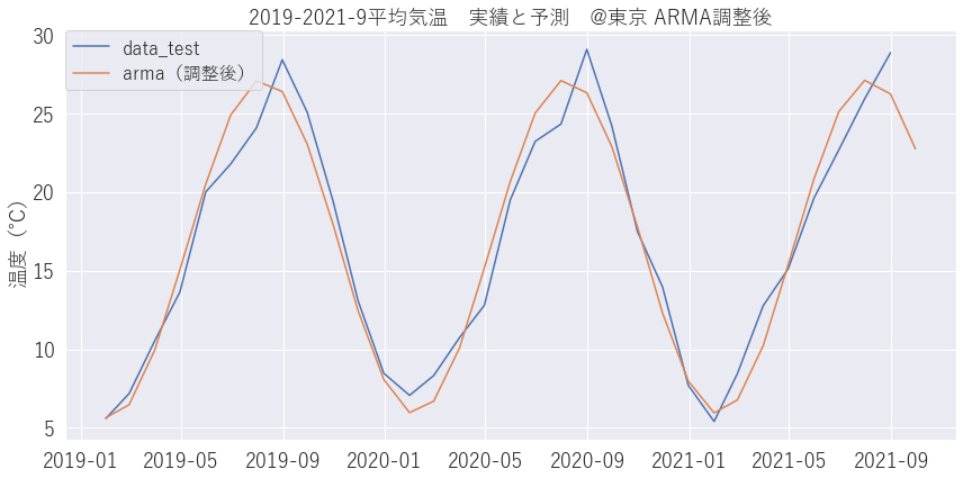
# ARMA p,q 調整後(月平均) 予測
model_arma = ARMA(train, order = [4,2])
result_arma = model_arma.fit()
prediction_arma = result_arma.predict(start=len(train), end=len(df_month))パラメータを調整し再学習させたところ、うまく予測できました。パラメータの調整って大事ですね。
ARIMAの予測結果
つづいてARIMAモデルで学習、予測をしてみましょう。
やり方はARMAとほとんど一緒ですが、ARIMAでは、ARの次数pは自己回帰部分の次数、MRの次数qは移動平均部分の次数に加え、Iの次数dを追加しています。dは差分の階数の次数をあらわしています。 下記コードでは[1,0,1]としていますが左からAR、I、MRをあらわしています。最初はとりあえず[1,0,1]で学習、予測してみます。
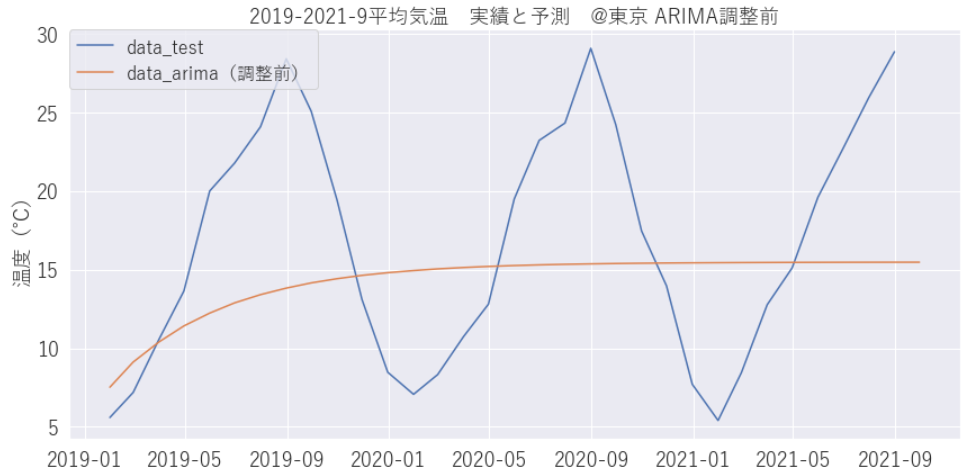
model_arima1 = ARIMA(train,order = [1,0,1])
result_arima1 = model_arima1.fit()
prediction_arima1 = result_arima1.predict(start=len(train), end=len(df_month))うーん、うまく予測できていません。パラメータの調整をしてみましょう。
ARIMA パラメータ調整
for文でaicが最小になるp,d,qを求めます。
# モデルの優劣の判定にAICという基準を使う
min_aic = 99999999
# 最もAICがよかった(小さかった)p,d,qを格納する
min_pdq = []
for p in range(4,7):
for d in range(0,3):
for q in range(1,3):
model_arima =ARIMA(train,order = [p,d,q])
try:
result_arima = model_arima.fit()
except:
print(p,d,q,"では収束しませんでした")
continue
result_arima_aic = result_arima.aic
print(p,d,q,result_arima_aic)
if result_arima_aic < min_aic:
min_aic = result_arima_aic
min_pdq = [p,d,q] 以上の結果、[4,0,2] と出力されました。あらためて学習、予測をしてみます。
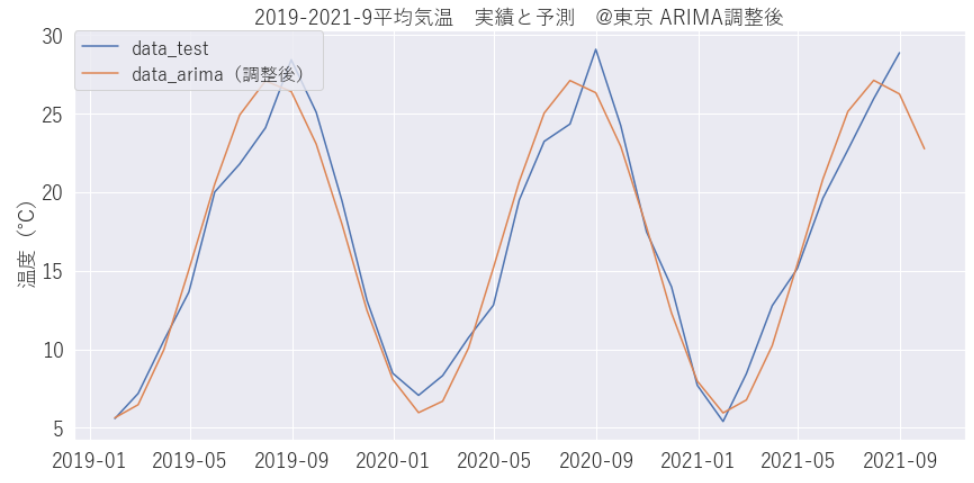
model_arima1 = ARIMA(train,order = [4,0,2])
result_arima1 = model_arima1.fit()
prediction_arima1 = result_arima1.predict(start=len(train), end=len(df_month))うまく予測できましたね。
SARIMAの予測結果
つづいてSARIMAモデルで学習、予測をしてみましょう。
やり方はARIMAとほとんど一緒ですが、SARIMAでは、ARIMAにSの季節周期性を加えています。その為には、あらたに4つの次数(sp、sd、sq、s)が必要となります。ここのsは季節の周期性をあらわす次数で1年の周期は12ヶ月なので12に固定しておきます。その他 sp、sd、sq の最適な数値をfor文を使ってAICが小さくなる組み合わせをみつけていきます。最初はとりあえず[1,1,1][1,1,1,12]で学習、予測してみます。 結果として、このパラメータでも予測はできましたが、最適なパラメータで求めていきましょう。
model_sarima =SARIMAX(train1, order = [1,1,1], seasonal_order=(1,1,1,12))
result_sarima = model_sarima.fit()
prediction_sarima = result_sarima.predict(start=len(train1), end=len(df))最適なパラメータを求めるには次のコードで行えます。
import itertools
p = q = range(0,3)
sp = sd = sq =range(0,2)
# p,q,sp,sqの組み合わせのリストを作成する。和分=1, 周期12は固定
pdq = [(x[0],1,x[1]) for x in list(itertools.product(p,q))]
seasonal_pdq = [(x[0],x[1],x[2],12) for x in list(itertools.product(sp,sd,sq))]best_result = [0,0, 100000000]
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = SARIMAX(train,order = param, seasonal_order=param_seasonal)
results = mod.fit()
print("ARIMAパラメータ{}, 季節変動パラメータ{} - AIC: {}".format(param,
param_seasonal, results.aic))
if results.aic < best_result[2]:
best_result = [param, param_seasonal, results.aic]
except:
continue
print("AIC最小のモデル:", best_result)結果として次のような組み合わせが最適なようです。この組み合わせて予測してみると下のようなグラフになります。うまく予測できていますね。
AIC最小のモデル: [(1, 1, 1), (0, 1, 1, 12), 224.63670925802757]
model_sarima =SARIMAX(train1, order = [1,1,1], seasonal_order=(0,1,1,12))
result_sarima = model_sarima.fit()
prediction_sarima = result_sarima.predict(start=len(train1), end=len(df))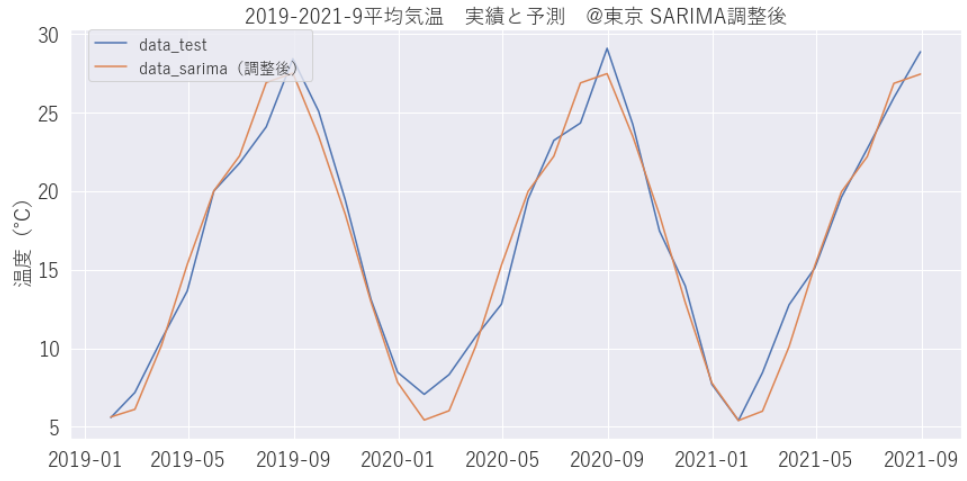
Prophetの予測結果
つづいては、今までのような統計モデルではなく、Facebookが開発した予測モデルProphetを使って予測をしてみましょう。
はじめに、モデルを定義します。引数には様々なパラメータを入力できます。詳細な調整をしたい場合はこのパラメータに変更を加えていきます。参考までに下記の記事にProphetについてまとめていますのでご興味がありましたらのぞいてみてください。
# モデルの定義
model_prophet=Prophet(
growth='linear',
changepoints=None,
n_changepoints=25,
changepoint_range=0.8,
yearly_seasonality='auto',
weekly_seasonality='auto',
daily_seasonality='auto',
holidays=None,
seasonality_mode='additive',
seasonality_prior_scale=10.0,
holidays_prior_scale=10.0,
changepoint_prior_scale=0.05,
mcmc_samples=0,
interval_width=0.8,
uncertainty_samples=1000,
stan_backend=None,)Prophetで予測する場合には、お決まり事として時系列データをds,目的変数をyに変更する必要があります。また、精度向上のためのパラメータの中に非線形予測もありますが、それを利用する場合には新たにcapのカラムを設ける必要があります。capは”capacity”で目的変数の予測される上限値を設定しておく必要があります。ここでは日本の最高気温は40℃を超えることはまずないのでおおよそ40℃程度と考えて、40と設定しておきます。
# dsとyを設定する
train_p = train_p.rename(columns={"年月日":"ds", "平均気温(℃)":"y"})
train_p["cap"] = 40 #実測値の最大値から40程度であれば予測最大値は入るだろうとしているデータフレームの中身はこんな形になります。
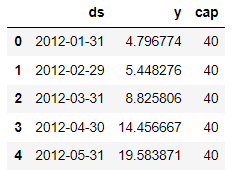
ここまでできたら、モデルの学習を行います。
通常の機械学習と同様、.fit()を使って学習します。また予測したい未来データを格納するための未来ボックスをあらかじめ作っておく必要があります。これもお決まり事として知っておきましょう。
# モデルの学習
model_prophet.fit(train_p)
# 将来の予測したいデータを用意する必要がある 箱を用意
future_month = model_prophet.make_future_dataframe(32, freq="M")
# 箱にもcapを設定する必要がある
future_month["cap"]=40予測する箱にもcapを設定しておく
予測します。うまく予測ができていますね。パラメータは結果的にデフォルトの状態が最もよかったようです。青い実線が予測値をあらわしており薄い青い面積を持ったものが80%信頼区間をあらわしています。これはデフォルトで80%となっていますが、interval_widthパラメータの調整により設定の変更は可能です。必要に応じ変更してみましょう。
# 予測してみる
forecast_month = model_prophet.predict(future_month)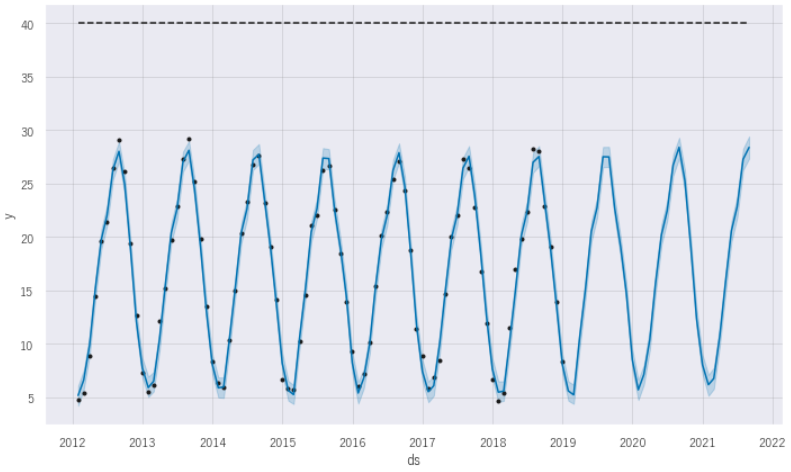
4.モデルの比較・検証方法
今までAR, ARMA, ARIMA, SARIMA, Prophetで予測してきました。それぞれのモデルで一応予測ができていたようですが、果たしてどのモデルが一番性能がよかったのでしょうか。定量評価をしていきたいと思います。評価指標はMAPE(メイプと呼ぶこともあります。)を使っていきます。
評価方法 MAPE(メイプ)
平均絶対パーセント誤差(MAPE:Mean Absolute Percentage Error)を使います。
MAPEとは各データに対して「予測値と正解値との差を、正解値で割った値(=パーセント誤差)」の絶対値を計算し、その総和をデータ数で割った値(=平均値)MAPEは直感的にどの程度ずれているのかが分かりやすい利点があります。
以下は、ARIMAモデルのMAPEの求めるコードです。
それぞれのモデルで得られた予測値を入れてMAPEを出力します。
# ARIMA(パラメータ調整後)のMAPE評価
# 結果を入力する空のデータフレームを用意する
res_arima = pd.DataFrame()
res_arima["y"] = prediction_arima1 # yに予測値を入力します。
res_arima["t"] = test # 比較する実測値(ここでは2019年~2021年までの実績データ)
res_arima=res_arima[:"2021-8-31"]
# 月平均 ARMAの予測結果の MAPE評価
y_true = res_arima["t"] # y_trueに代入
y_pred = res_arima["y"] # y_predに代入
# MAPEの関数に入力する
def mean_absolute_percentage_error(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_pred - y_true) / y_true)) * 100
mean_absolute_percentage_error(y_true, y_pred)MAPEでの 比較結果
以下のような結果になりました。月平均での予測を実施してきましたが最も当てはまりがよかったモデルはSARIMAモデルになりました。また意外にも単純なモデルのARでもそこそこの結果が出ています。今回扱った気温データでは、そこまで大きな差はなかったようです。
また、今回の予測では日平均は書いていませんでしたが、下表にある通り日平均でも予測をしています。しかし、AR,ARIMA,SARIMAではパラメータの調整もむなしく予測ができませんでした。対数化や差分を取ることで予測した方がいいかもしれません。
| MAPE(%) | AR | ARMA | ARIMA | SARIMA | Prophet |
| 月平均 | 8.55 | 8.97 | 8.97 | 7.74 | 8.18 |
| 日平均 | – | 18.21 | – | – | 20.24 |
まとめ
最後まで読んでいただきありがとうございました。時系列予測の基本的な扱い方はごりかいいただけたかなと思います。今回は周期性も非常にわかりやすい気温のデータで解説を進めましたが、みなさんのご興味のあるデータ、業務で応用できそうなデータがございましたら時系列予測を実践してみてもおもしろいのではないでしょうか。わたしも今後は、台風などの発生予測や年賀状の発行枚数などなどいろんなデータで楽しみながら未来予測をしてみたいと思います。自分の人生も正確に予測できたらなぁと今回のデータ解析をしながらつくづく思いました。

まだまだ勉強不足の面は否めませんが基本的な時系列モデルの比較を実施してみました。いずれのモデルでも実装に関しては非常に簡単です。実際に業務に使おうと思ったらさまざまなパラメータの調整やデータの準備が必要になりますが、ひとつの参考としてお役に立てていただければ幸いです。

今後は、もっと時系列分析の理解を深めることと、RNNやLSTMといったディープラーニングの時系列分析も学習していけよ!

がんばります!!!




コメント