100年分の地震データでProphetの時系列予測をしてみた

この記事は、こんな方におすすめです。

PythonでProphetを使ってみたい、初めて使ってみるという方
地震の予測にチャレンジしてみたい方
地震データを入手してみたい方

はじめに
- 地震発生予測のすすめ方
約100年分、震度3以上の地震データを入手する方法
データの前処理方法
学習データとテストデータに分割する
予測モデルの構築をする方法
- Prophetのパラメータの説明
- モデルに学習させる方法
Prophetを使った地震発生予測をする方法
精度評価結果
まとめ

はじめに

ご訪問いただきありがとうございます。本記事では、Facebookが開発したPythonやRで実装可能な時系列予測ソフトウェア「Prophet」を使い地震の発生予測をおこなっていきます。この予測を通してProphetの簡単な使い方を解説していきたいと思います。聞いたことがあり興味があるけどよくわからないという方やProphetを今後使っていきたいという方のお役に立てれば幸いです。
　また、今回は、地震の発生予測をおこなうにあたって、気象庁のデータを参考にさせていただきましたが、これらのデータの見方、入手方法についても解説していますので、ご自身で地震データの入手したいという方にもおすすめの記事になっています。それでは、地震の発生予測をしていきましょう。出来たらすばらしいですよね。

なお、Pythonを中高年が基礎から最速独学で学ぶ方法を別の記事でまとめていますので、よろしければご覧ください。>> 中高年の為の挫折しない最短のPython,AI・機械学習のおすすめ学習方法
>> 中高年がAI・機械学習を学ぶ為のプログラミングスクール　主要8校を徹底比較

地震発生予測のすすめ方

具体的には、次のようなステップで進めます。ひとつひとつ解説していきます。

約100年分、震度3以上の地震データを入手する
データの前処理を行う
学習データとテストデータに分割する
予測モデルを構築する
Prophetを使った地震発生を予測する
精度評価
まとめ

約100年分、震度3以上の地震データを入手する方法

データソースは、気象庁の震度データベースのサイトから入手させていただきます。こちらから訪問可能です。

震度データベース検索

気象データベースでは、下図のような画面であらわされ、1919年の観測開始からのデータを閲覧することができます。地図上の丸の大きさでマグニチュードの大きさをあらわし、色で震度の深さをあらわしています。右側の検索ボックスで、地震発生日時、震度別地震回数、最大震度の大きさなどが設定でき、そのまま地図上にバブルプロットであらわされるため、視覚的にも直感的にも非常にわかりやすくつくられています。ご興味がありましたら、グラフを操作してみるとオモシロいですよ。

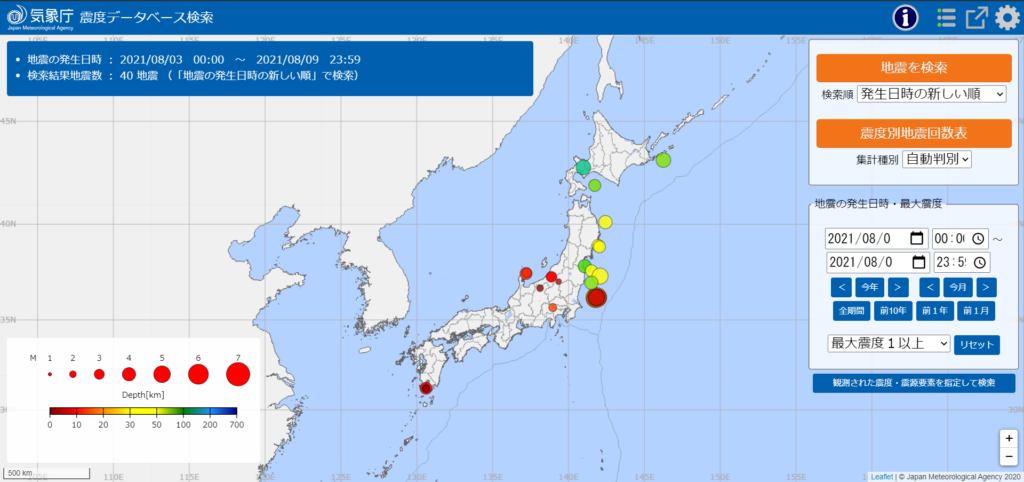
前置きが長くなってしまいましたが、過去の地震データの入手方法ご説明いたします。

画面右側の検索ボックスでご自身で入手したい任意の期間、地域、震度などの検索条件を入力し右上の「地震を検索」ボタンをクリックします。

震度データベースの右上の検索ボックスです。 — 震度データベースの右上の検索ボックス

地図上に円形のバブルプロットが表示されます。これらのデータを入手するには、右上のリストのアイコンをクリックします。するとバブルプロットで表されたリストが表示され、最下段までスクロールすると「CSVファイルダウンロード」のボタンがあらわれますので、こちらからCSVデータとして入手することができます。

データをリスト化するアイコン

データの最下段にcsvダウンロードのボタンがあります。 — データの最下段にcsvダウンロードのボタンがあります

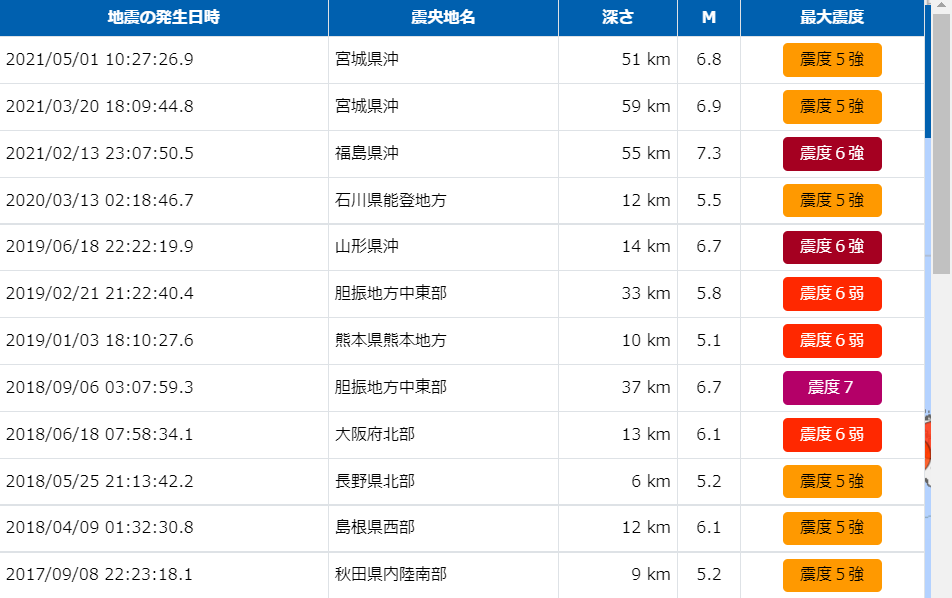
ただしCSVファイルは一度のダウンロードで1,000行分のデータしか入手できないので、検索条件によっては面倒ですがダウンロードを繰り返さなくてはいけません。

今回、予測に使いたいデータは1919年から2021年8月までの約100年分、全国で発生した震度3以上のデータです。データファイルとして全15ファイルをダウンロードしました。

ただ、この15ファイルをひたすら合体（concat）させるのも面倒ですので、Pythonの便利な関数「glob関数」を使用します。特定条件に従ったファイルを一括で取得する場合に非常に便利ですので覚えておきましょう。まずは、osとglobをインポートしておきましょう。そしてos.chdir()の引数にはファイルが格納されているディレクトリを指定してあげます。今回の例ではダウンロードした15個のファイルの名称を「地震リスト1～15」と割り振り、for文で特定する条件として＊地震リスト＊とついているファイルを全て読み込むようにしておきます。

import os
import glob
os.chdir(ファイルが格納されているディレクトリ)
df = pd.DataFrame(columns = [])
for i in glob.glob("*地震リスト*"):
    tmp = pd.read_csv(i)
    df = pd.concat([df, tmp])

glob関数を使い、特定条件でファイルを指定するだけ。たった5行のコードで100年分のデータを一瞬でデータフレーム化してしまいました。プログラミングってやはりスゴいですね～

データの前処理方法

続いてはデータの前処理です。100年分のデータをCSVデータで入手し、glob関数で一つデータフレームに落とし込みました。では100年分のデータの中身を確認していきます。下表のように発生時刻や緯度、経度まで詳細な地震データが確認できます。

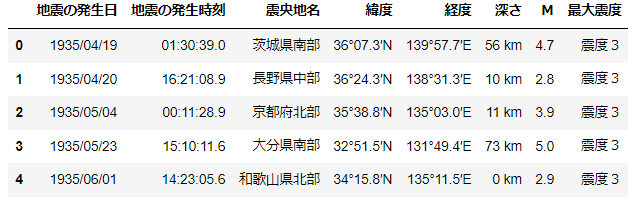
入手したデータをPythonで読み込んだものです。 — 入手したデータをPythonで読み込んだもの

次に、Prophetを使うにあたり、時系列として認識させてあげなければいけないので、地震の発生日と発生時刻を結合してdatetime型に変更し”ds”という変数にいれてあげます。Prophetでは決まりとして時系列データを”ds”、目的変数を”y”として格納してあげる必要があります。
また、震源の深さや最大深度がstr型であった為、intもしくはfloat型の数値データに変換します。
ちなみに今回のデータ数は15,263行、8列です。

【datetime型に変換する】

# datetime型に変換する
from datetime import datetime as dt
datetime = dt.strptime(str_datetime, "%Y/%m/%d %H:%M:%S")
datetime
# for文適用
datetimes = []
for index, datum in df1.iterrows():
    date = datum["地震の発生日"]
    time = datum["地震の発生時刻"]
    str_datetime = f"{date} {time}"
    datetime = dt.strptime(str_datetime, "%Y/%m/%d %H:%M:%S")
    datetimes.append(datetime) # datetimesというリストに格納する
df1["ds"] = datetimes # 新しいdsというカラムに格納する

次に、Prophetで予測するためには、目的変数としてy, 時間データとしてdsを設定する必要がある

y＝マグニチュード
ds= 年月日時間

変換後のデータはこんな感じ。元の地震の発生日、発生時刻は消していた方がスマートかもしませんね。ここでは、そのまますすめちゃいます。

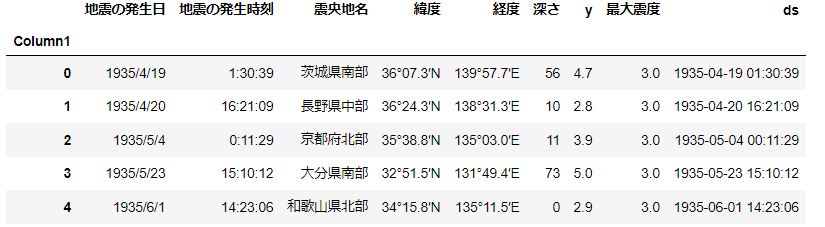
Prophet用にdsとyを加えたリストです。 — Prophet用にdsとyを加えたリスト

学習データとテストデータに分割する

次に学習データとテストデータに分割します。このやり方は、通常の機械学習と考え方は一緒です。分け方は、holdoutやkfoldといったランダムに分割するのではなく、単純に時系列で区切っています。過去からの経緯で予測しようとすると自然です。今回は、以下の通り、1919年～2019年の約100年分を学習データとしてそれ以降のデータをテストデータとしてみます。このあたりは、任意で期間を変更して試していただければいいかなと思います。評価は、学習モデルで予測した2020年以降のデータと実績データを比較し精度の評価をしてみたいと思います。

・学習データ＝　13,494　　…1919年～2019年までのデータ
・テストデータ=  299　　　…2020年～2021年8月までのデータ

予測モデルの構築をする方法

あらかじめprophetをインストールしてあることが前提になります。
prophetをインストールする前にあらかじめ「ephem」,「PyStan」をインストールしたうえでprophetをインストールします。インストール手順は次の通りです。

condaの場合

conda install -c anaconda ephem
conda install -c conda-forge pystan
conda install -c conda-forge fbprophet

pipの場合

pip install ephem
conda install -c anaconda ephem
pip install fbprophe

prophetをインポートし、モデルを定義付けます。その際に引数として設定可能なパラメータが入力されていますが、最初はデフォルトで実施してみます。パラメータの詳細は以下の通りです。ここではパラメータの調整は行いませんが、下記を参考にご自身で探ってみるのもおもしろいと思います。

Prophetのパラメータの説明

growth:
線形または非線形の予測が選択できます。非線形を選択する場合はcap（トレンドの上限）を設定してあげる必要があります
changepoints:
変更点の候補を含める日付のリスト。指定しない場合、潜在的な変更点が自動的に選択されます
n_changepoints:
潜在的な変化点の数。変化点が指定されている場合は使用されません。変化点が指定されていない場合、潜在的な変化点は、履歴の最初のchangepoint_range割合から均一に選択されます。大きければ大きいほど多くの変化点が検出されやすくなります。デフォルトは25
changepoint_range:
トレンド変更点が対象となる履歴の割合が推定されます。最初の 80% のデフォルトは 0.8 です。変更点が指定されている場合は使用されません。公式によると[0.8、0.95]の範囲が妥当
yearly_seasonality:
毎年の季節性にフィットします。Auto、True、False、またはフーリエ級数を指定できます
weekly_seasonality:
毎週の季節性にフィットします。Auto、True、False、またはフーリエ級数を指定できます
daily_seasonality:
毎日の季節性にフィットします。Auto、True、False、またはフーリエ級数を指定できます。
holidays:
カラムにholiday(string型)とds(datetime型)とオプションで休日の2日前であるlower window と休日として含める日付の前後の日数の範囲を指定するupper windowを設定できる。また、オプションで、その休日の前のスケールを指定する列prior_scaleを持つことができます
seasonality_mode:
季節性のモードの切り替えです。デフォルトはaddictiveとなっており、multiplicativeが選択可能であり、徐々に周期的に増加するような事象の場合にその増加し続ける周期性をモデリングすることができます
seasonality_prior_scale:
季節性モデルの強度を変調するパラメータです。値が大きいほど、モデルはより大きな季節変動に適合し、値が小さいほど季節性が低下します。add_seasonalityを使用して、個々の季節性に指定できます。デフォルトは10で、公式によると[0.01、10]の範囲が妥当
holidays_prior_scale:
休日の入力でオーバーライドされない限り、休日コンポーネントモデルの強度を変調するパラメータ。
changepoint_prior_scale:
自動変化点選択の柔軟性を変調するパラメータ。大きな値は多くの変更点を許容し、小さい値は変更点を少なくします。つまり小さすぎるとトレンドが不十分であり、大きすぎるとオーバーフィットしてしまう。デフォルトは0.05で、公式によると[0.001、0.5]の範囲が妥当
mcmc_samples:
Integerが0 より大きい場合は、指定された数の MCMC サンプルでベイズ推論を行います。0 の場合は、MAP 推定を行います
interval_width:
浮動小数点数、予測に対して提供される不確実性区間の幅。mcmc_samples=0 の場合、外挿生成モデルの MAP 推定値を使用したトレンドの不確実性に過ぎません。mcmc.samples>0 の場合、すべてのモデルに統合される季節性の不確実性を含むパラメータです
uncertainty_samples:
不確定間隔を推定するために使用されるシミュレートされた描画の数。この値を 0 または False に設定すると、不確定性推定が無効になり、計算速度が速くなります
stan_backend:
すべての利用可能なバックエンドを反復処理し、作業しているバックエンドを見つけます

# Prophetを利用した予測
from fbprophet import Prophet
from fbprophet.plot import add_changepoints_to_plot
model = Prophet( growth='linear',
    changepoints=None,
    n_changepoints=25,
    changepoint_range=0.8,
    yearly_seasonality='auto',
    weekly_seasonality='auto',
    daily_seasonality='auto',
    holidays=None,
    seasonality_mode='multiplicative',
    seasonality_prior_scale=20.0,
    holidays_prior_scale=10.0,
    changepoint_prior_scale=0.05,
    mcmc_samples=0,
    interval_width=0.8,
    uncertainty_samples=1000,
    stan_backend=None,)

モデルに学習させる方法

定義づけたモデルで2019年以前のデータで学習します。学習は一瞬で完了します。100年分とはいえ、コンピュータにとっては何てことはない作業でした。本当に学習できているのか楽しみです。

df_train = df[df["ds"] <= dt(2020,1,1,0,0)]
model.fit(df_train)

Prophetを使った地震発生予測をする方法

つづいて、予測する箱を用意します。Prophetの考え方として、予測したい未来をあらかじめ時系列で用意してあげる必要があるのです。ここでは仮に800日分の未来を予測しますが、200日でも1000日でも任意に決めることができます。ただし、pandasの設定上2258年以上の設定はできませんので注意が必要です。それ以上に設定しようとするとエラーが返ってきてしまいます。コード中のfreq=Hとは1時間単位での予測としています。ここもDでは日単位、Mは月単位、Yは年単位と任意に変更が可能で、大文字でも小文字でも認識可能です。色々と試してみると理解が深まります。では.tail()で中身をみてみましょう。2020年1月から800日後として約2年2か月分の未来の箱を用意できました。

# 将来の予測したいデータを用意する必要がある 箱を用意
future = model.make_future_dataframe(24*800, freq="H") 
future.tail()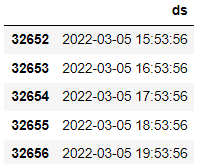

それでは、ようやくですが予測してみましょう。
予測では、さきほど学習したmodelで800日分の未来を格納したfutureをpredictしてみます。
可視化は、model.plot(forecast)で可能です。x軸はplt.xlimで任意の設定が可能です。

# 予測してみる
forecast = model.predict(future)
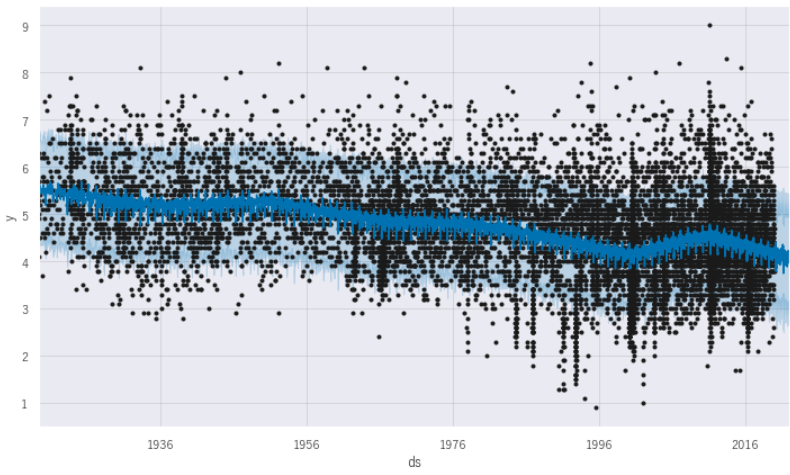
model.plot(forecast)
plt.xlim(dt(1919,5,1), dt(2021,12,31))
plt.show()

x軸が年月日をあらわし、y軸がマグニチュードをあらわしています。黒丸は実績で中央に走っている青い線が予測線をあらわしています。薄い青色の範囲が95％の不確実性をあらわしています。1919年からプロットしている下グラフをみると、地震の測定定義の変更などにもよりますが地震発生時のマグニチュードは小さくなっている傾向にありますね。また、黒い点をみると1990年代後半からは多く発生しているようにもみえます。右端の黒点のない範囲が今回の未来予測部分です。実績は2021年8月まででしたので、それ以降、2022年3月までの予測です。今までの傾向を踏襲して下降傾向にみえます。

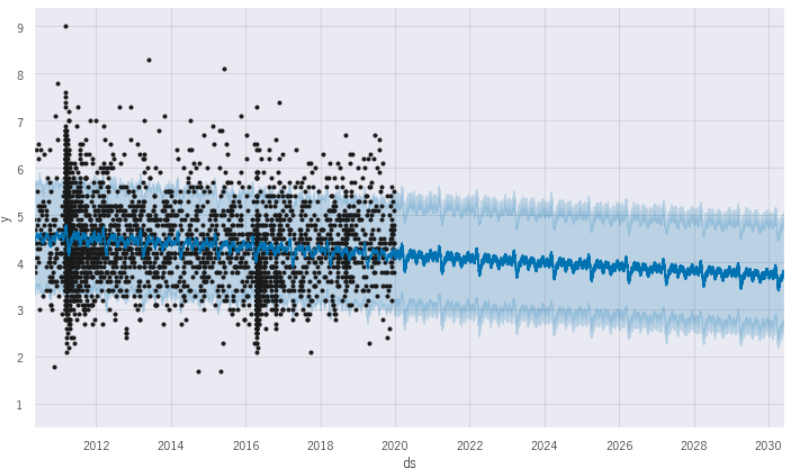
さらに未来の箱の範囲を延長して、拡大してみます。2010年5月～2030年までの予測値をみてみましょう。マグニチュードは徐々に低下傾向にあります。しかし実測値をみると必ずしも95％の不確実性の範囲内に収まっているわけではないので、予測とはいいがたいですね。

Prophetで予測したグラフです。拡大版です。 — Prophetで予測したグラフ

つづいて予測の概要をみてみましょう。components関数で予測全体のトレンドと週間、年間、時間単位での発生傾向を確認できます。

model.plot_components(forecast)
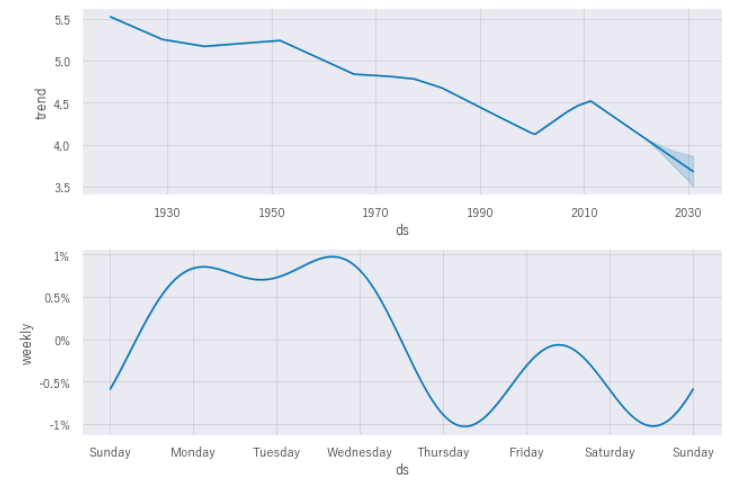
plt.show()

trendでは、徐々に減少傾向であることが見受けられます。
weeklyでは、偶然かもしれませんが月～水にかけて地震が発生する可能性が高いようです。ちなみに2011年3月11日は”金曜日”でした。
yearlyでは、特に3月に発生することが多いようです。
dailyでは、14時前後から18時あたりに起きることが多そうですね。
そう言われればそうかもしれませんが、あまり実感がわかずピンとこないですね。

上からTrend、周期性をのぞいた傾向がみえます。下段がweekly、ここでは週間での地震の起きやすさがわかります。 — 上からTrend、周期性をのぞいた傾向がみえます。下段がweekly、ここでは週間での地震の起きやすさがわかります

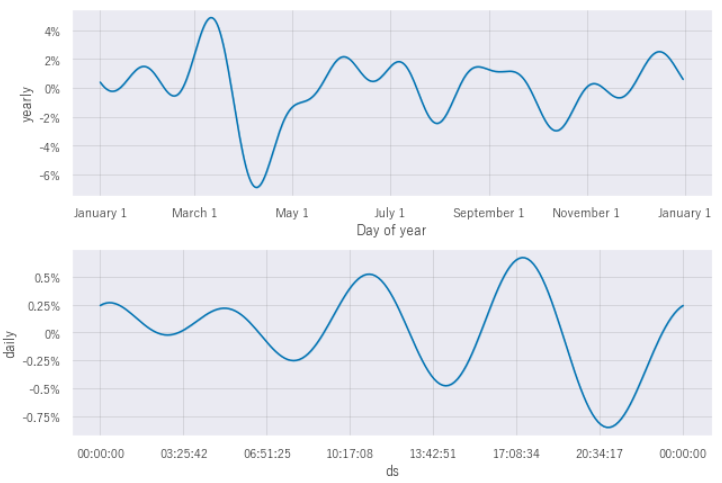
上からyearly、ここでは月別に地震の起きやすさをあらわしています。下段では、dailyで地震の発生時間帯をあらわしています。 — 上からyearly、ここでは月別に地震の起きやすさをあらわしています。
下段では、dailyで地震の発生時間帯をあらわしています。

順番が逆かもしれませんが、マグニチュードには何らかの自己相関があるかどうかをコレログラムで確認してみます。コレログラムとは、自己相関グラフで時系列的に周期性の相関があるかどうかをみることができます。

import statsmodels.api as sm
plt.rc("figure", figsize = (12,6))
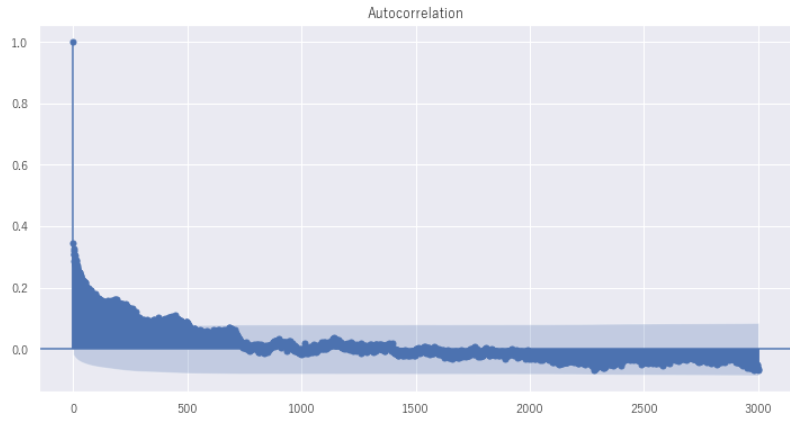
res = sm.graphics.tsa.plot_acf(df["y"],lags = 3000)
# x 軸がどの程度ずらしているかをあらわし、y軸に相関の強さを表している

x軸はデータ数を表しており2019年から2021年までを表しています。相関があればウネウネとした周期性をもった形があらわれるのですが、下図ではほとんどそのような周期的な動きをしているようにはみえません。従って自己相関はみられず、地震のマグニチュード発生には周期性はみられないと考えられます。

自己相関図（コレログラム）です。地震の発生に周期性があれば縦軸の値は高くなります。 — 自己相関図（コレログラム）です。地震の発生に周期性があれば縦軸の値は高くなります

精度評価結果

あらかじめ分けておいた2020年以降の実績と予測値をMAPEで評価します。回帰などの予測評価では一般的にRMSEやMSE、r2などが使われますが時系列予測ではどの程度ずれているのかピンときません。そこで時系列予測の評価基準でよくもちいられるのがMAPEです。これは誤差を割合で示してくれるため直感的にどれだけずれているかがよくわかります。

MAPEとは？
平均絶対パーセント誤差（MAPE：Mean Absolute Percentage Error）各データに対して「予測値と実績値との差を、実績値で割った値（＝パーセント誤差）」の絶対値を計算し、その総和をデータ数で割った値（＝平均値）を出力する関数である。

forecast_2020 = forecast[forecast["ds"] >= dt(2020,1,1)].reset_index(drop=True)
forecast_2020["yhat"].head() # yhat = 予測値のこと
# 結果を入力する空のデータフレームを用意する
results = pd.DataFrame()
# 実測値
results["t"] = df_test["y"]
# 予測値
results["y"] = forecast_2020["yhat"]
results["diff"] = results["t"]-results["y"]
results.head()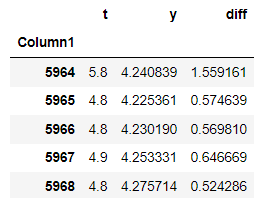

np.mean(abs((results["y"]-results["t"])/results["y"])*100)

結果として14.5％の誤差で予測ができているとの評価になります。しかし毎年マグニチュード3～6程度の地震は、国内のどこかでは必ずと言っていいほど起きているので、この値が意味をなしているかは正直、微妙です。

14.533706693462262

まとめ

　最後まで読んでいただきありがとうございます。今回は身近な地震のデータを通してProphetの初歩的な使い方を解説、実践してみました。今回の作業の80％くらいは、データの取得と前処理に時間を費やしました。ここで扱ったglob関数などを活用してできるだけ効率的に前処理をおこなっていきたいですね。また今回、パラメータ調整はおこないませんでしたが、調整しだいで精度の向上は見込まれますので、ぜひ挑戦していただきければと思います。まだまだ分析としてはやらなくてはいけないことはありますが、Prophetの基本的な使い方はご理解していただけたかと思います。少しでも皆さんの業務の一助になれば幸いです。
今回はここまでです。それでは、失礼します。