- Pythonの初学者で、機械学習に興味がある方
- 熱中症の予防をしたい方
- 熱中症の予測をしてみたい方
はじめに
ご訪問いただき、ありがとうございます。本記事ではPythonの機械学習ライブラリを使って東京の熱中症の過去データから予測モデルを作成してみたいと思います。この熱中症データの機械学習モデルの作成を通して、Pythonによる機械学習の基本的な使い方を解説していきます。また、熱中症データの分析をしていくことで、熱中症にかからないために気を付けなければならないポイントもあきらかになってきます。自分は大丈夫と思っていても気付かないうちにかかってしまうとっても怖い傷病ですが、十分防止はできますので気を付けてすごしましょう。
なお、Pythonを中高年が基礎から最速独学で学ぶ方法を別の記事でまとめていますので、よろしければご覧ください。>> 中高年の為の挫折しない最短のPython,AI・機械学習のおすすめ学習方法
>> 中高年がAI・機械学習を学ぶ為のプログラミングスクール 主要8校を徹底比較
熱中症予測モデル作成の進め方
それでは、次のようなステップですすめていきたいと思います。一つ一つ確認しながら進めていきましょう。
- データソースの確認する
- データの内容を確認する
- 各特徴量と熱中症の相関関係を確認する
- Pythonを使った機械学習で予測モデルを作成、評価する
1.データソースはこちら
今回は区切り良く2011年から2020年までの10年分の気象データおよび、総務省消防庁がまとめている熱中症による救急搬送人数のデータを用います。熱中症患者数の推移は2008年からデータがありますのでご興味がある方はのぞいてみてはいかがでしょうか。ただ、気象データと熱中症データをそれぞれ合体させる必要があるのですが、これが結構大変な操作でしてPythonでやることも可能なのですが今回は、使い慣れているExcelのクエリで合体をさせておきました。下記にダウンロードができるようしておきますので必要な方はご自由にお使いください。
総務省消防庁 熱中症情報
国土交通省気象庁 過去の気象データ・ダウンロード
2.データの内容を確認する方法
ここでは、機械学習をする前にデータの中身をみて自分自身の目でどのようなことが起きているのか俯瞰(ふかん)することを行います。データ分析の世界ではこの段階のことをEDAと言われます。EDAとは「Explanatory Data Analysis」の頭文字をとったもので、日本語では探索的データ分析と言います。この段階でおおよそのデータの概要をつかみ、解決すべき課題に対するアプローチを考える地味ながらも非常に大事なステップになります。
熱中症による救急搬送人数の推移
下グラフー1は、2011年~2020年までの東京における熱中症による救急搬送人数の推移をあらわしています。2018年からの3年間はそれまでの都市と比べると熱中症が多くなっていますね。また高齢者に特に多く発症していることがわかります。
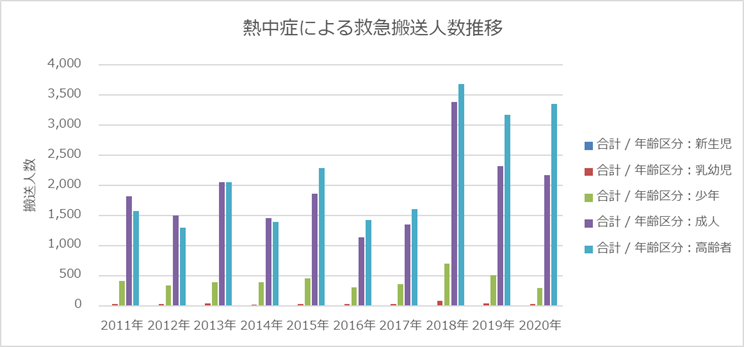
熱中症の傷病程度別の推移
下グラフー2は、熱中症の傷病程度別にみたグラフになります。中軽症がほとんどで重症、死亡に至るケースは比較的少ないといえます。とはいえ死亡者も一定数いますので油断は禁物です。
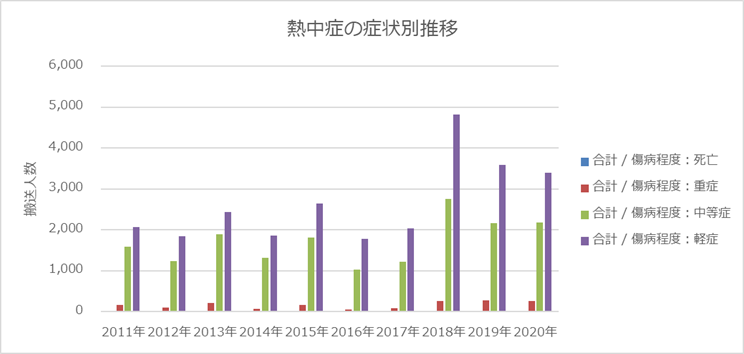
熱中症の発生場所ごとの搬送人数
下のグラフー3では、熱中症の発生場所ごとの搬送人数をしめしています。(データを取り始めたのが2017年から)最も多いのが住居、次いで道路、公衆(屋内)となっています。住居では知らず知らずのうちに熱中症になってしまっているケースが多いようです。うちにいるから大丈夫とはいえませんね。こまめな水分補給を心掛けましょう。また道路とは、特に道路工事や交通整理などに従事する方に多いものと予想されます。また公衆(屋内)とは、劇場、コンサート会場、飲食店、百貨店、病院、公衆浴場、駅(地下ホーム)等を指しています。
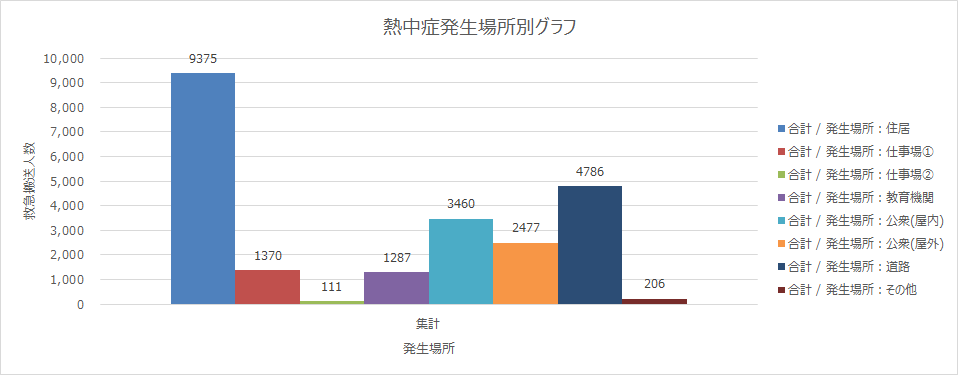
詳しくは、東京消防庁のHPでデータから見解を公開しております。
温度差と熱中症の関係
下グラフー4は、2011年~2020年までの気温データ(平均、最高)と搬送人数の時系列グラフです。特に2018年から気温差が大きくなっているようで、また搬送される方もふえているようにもみえます。ギザギザにみえているのは、熱中症データは各年6月~9月のデータで構成されており12か月分のデータはないためです。
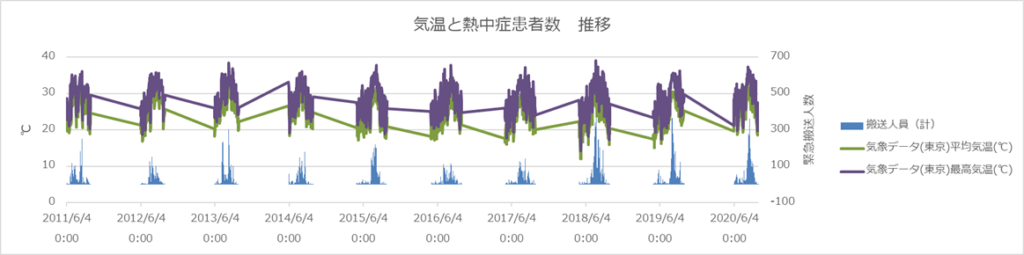
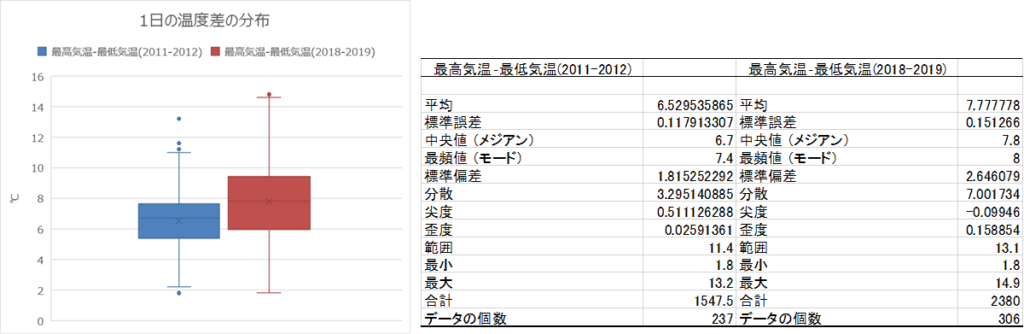
そこで、10年前の状況と直近のデータを比べる為に2011-2012と2018-2019のそれぞれ2年間分の1日の最高気温と最低気温の差の分布をみてみます。下左の図は、箱ひげ図で青い箱が2011-2012、赤い箱が2018-2019をあらわしています。赤い箱の方が大きいことから2018-2019の方が温度差は全体として大きい。また最大をあらわすひげの一番上も大きく上昇していることがわかり、やはり2018-2019の温度差の大きいことがあきらかです。(後ほど機械学習に特徴量として使いましょう)
各特徴量と熱中症の相関関係
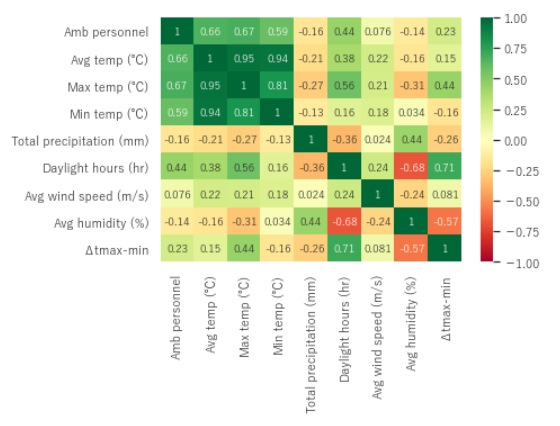
ここでは、それぞれの特徴量の熱中症による救急搬送人数との相関関係をみていきます。相関関係を直感的に把握しやすいヒートマップに図示してみましょう。下図-1の「Amb personel」が救急搬送人数を表しています。
この相関関係をみると、特に気温,Avg temp(平均気温)、Max temp(最高気温)、Min temp(最低気温)との相関係数が0.59~0.67と相関がありそうです。また上述した温度差「⊿tmax-min」と救急搬送人数の相関をみると0.23とそこまで大きな相関はなさそうです。その代わり日照時間(Daylight hours)が0.44と相関がありそうだということがわかりました。
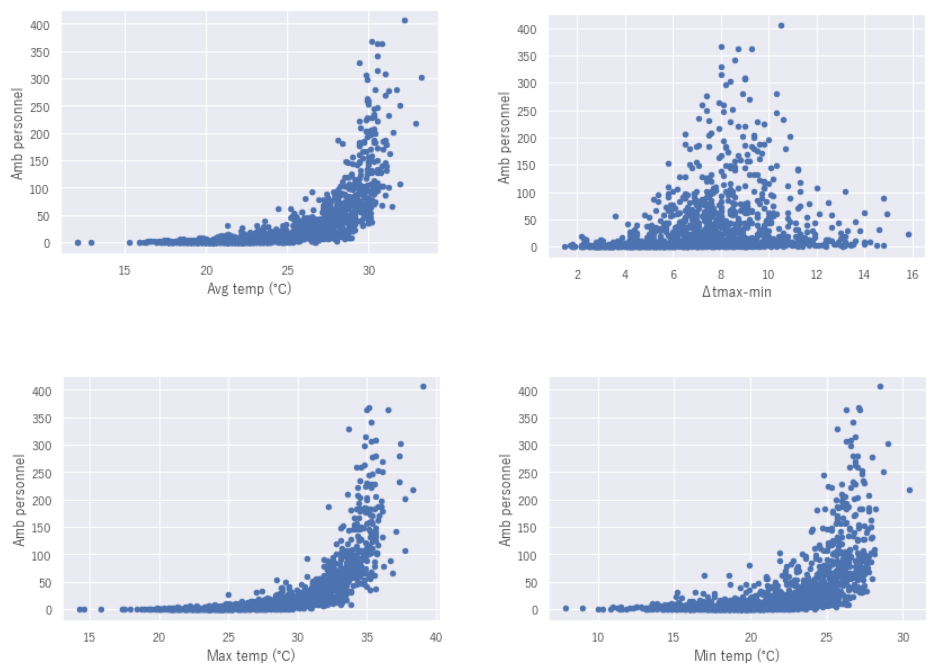
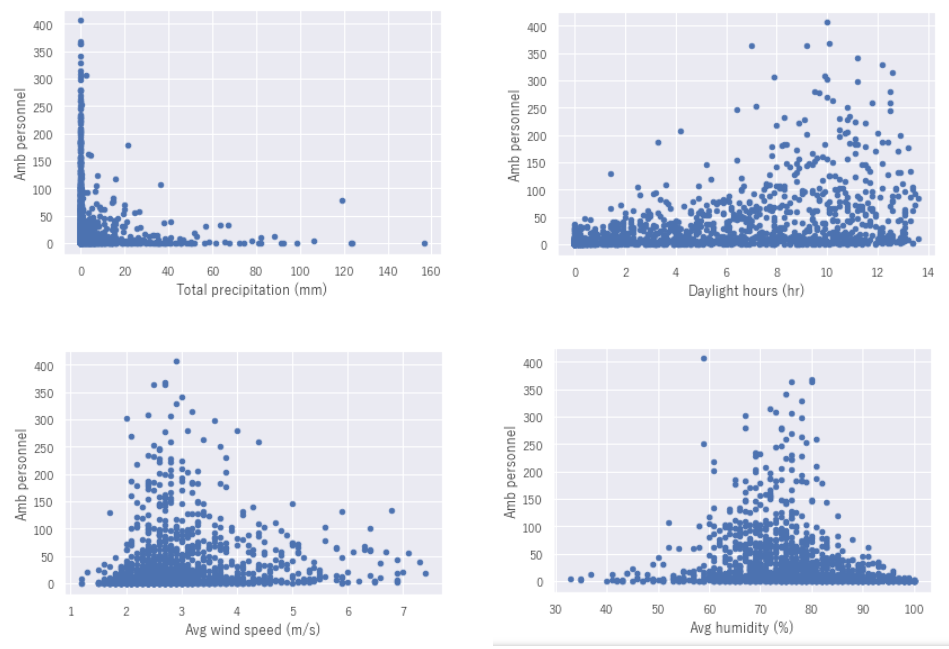
各特徴量と熱中症数の散布図
相関のありそうな項目を散布図としてあらわしてみます。すると気温(Avg,Max,Min)は温度の上昇とともに指数関数的に熱中症の救急搬送数が上昇していることがわかります。気温差(⊿Tmax-min)は8~10℃の気温差があるときに救急搬送数が増加傾向にあるようです。湿度(Avg humidity)は、そこまで大きな相関はグラフからみてもわかります。次にこれらの特徴量を使って機械学習を行っていきます。
Pythonを使った機械学習の方法
いよいよPythonを使って機械学習のモデルを作成していきます。今までみてきたそれぞれの特徴量と熱中症による救急搬送人数を使っていきましょう。
データの読み込み
冒頭に作成したデータを読み込みます。
df = pd.read_excel("熱中症患者数2011-2020.xlsx",sheet_name = "Sheet1") データを説明変数x、目的変数t に分割する
説明変数では、最終的に降水量の合計「Total precipitation(mm)」は、モデルの性能に寄与しなかったため除外しました。目的変数は救急搬送人数(Amb personnel)としています。
train_val, test = train_test_split(df, test_size = 0.2, random_state=0)
# train_val を説明変数x, 目的変数t に分割する
x = train_val.drop(["Amb personnel","Total precipitation (mm)"],axis=1)
t = train_val[["Amb personnel"]]KFoldの処理で分割時の条件を指定し、cross_validate 関数で交差検証を行う
今回の予測アルゴリズムは、all_estimatorという網羅的に最適なアルゴリズムをチェックするライブラリを使って評価の高かったランダムフォレストを採用しました。コードは掲載していませんが下記ブログ記事を参考に実施しています。
from sklearn.model_selection import KFold
kf = KFold(n_splits= 4, shuffle= True, random_state= 0)
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate
from sklearn.model_selection import train_test_split, GridSearchCV
model = RFR()
result = cross_validate(model, x, t, cv = kf, scoring = "r2", return_train_score = True)
print(result)
# 平均値を算出する
sum(result["test_score"])/ len(result["test_score"])
# 結果:0.800473439357555検証段階でのスコアはr2で0.8程度とまずまず。念のためハイパーパラメータの調整を行います。
ランダムフォレストのチューニングを行う
グリッドリサーチで主要パラメータを総当たりさせて最も精度のよいパラメータの組み合わせを算出してくれます。今回は次のような結果になりました。
max_depth=15, max_features=6, min_samples_split=3, n_estimators=20, n_jobs=1,
rg = RFR(n_jobs=-1, random_state=2525)
rg.fit(x,t)
search_params = {
'n_estimators' : [5, 10, 20, 30, 50, 100],
'max_features' : [i for i in range(1,x.shape[1])],
'random_state' : [2525],
'n_jobs' : [1],
'min_samples_split' : [3, 5, 10, 15, 20, 25, 30, 40, 50],
'max_depth' : [3, 5, 10, 15, 20, 25, 30, 40, 50]
}
gsr = GridSearchCV(
RFR(),
search_params,
cv = 3,
n_jobs = -1,
verbose=True
)
gsr.fit(x, t)
print(gsr.best_estimator_)
# 結果:
# RandomForestRegressor(max_depth=15, max_features=6, min_samples_split=3,
n_estimators=20, n_jobs=1, random_state=2525)ベストパラメータで調整する
さっそく、ベストパラメータをランダムフォレストの引数に入力して再度クロスバリデーションをしてみます。すると
model1 = RFR(max_depth=15, max_features=5, min_samples_split=3,
n_estimators=20, n_jobs=1, random_state=2525)
result = cross_validate(model1, x, t, cv = kf, scoring = "r2", return_train_score = True)
print(result)
sum(result["test_score"])/ len(result["test_score"])
# 結果:0.8014893907821706ハイパーパラメータの調整、クロスバリデーションを行った結果、性能は0.800→0.801に微増。それほど劇的には性能は向上しませんでしたが、今回はこれでモデル完成とします。
訓練、検証データをまとめて通常の学習を行う
チューニングされたモデルで元の学習データの評価を行うと0.97という結果です。これは学習データそのものですので高い評価なのは当然の結果です。
model1.fit(x,t)
print("学習データ", model1.score(x,t))
# 学習データ 0.972910569298095作成したモデルでテストデータを評価してみる
では、次に最初に分割しておいたtestデータで検証をしてみます。この未知のデータで性能がでれば優秀です。testデータをtrainデータと同様に説明変数と目的変数に分けて今までチューニングしたモデルで評価をしてみます。するとr2で0.81とまずまずの結果に。さらにRMSEの結果をみると3.46と誤差が平均的に3~4人程度とそこまで悪くない予測ができたかなと思います。
# test を説明変数x, 目的変数t に分割する
x_test = test.drop(["Amb personnel","Total precipitation (mm)"],axis=1)
y_test = test[["Amb personnel"]]
# R2評価
model1.score(x_test, y_test)
# R2:0.8143483128494527
from sklearn.metrics import mean_absolute_error # MAE の計算
pred = model1.predict(x_test)
mae = mean_absolute_error(pred, y_test)
# RMSE 評価
import math
math.sqrt(mae)
# RMSE : 3.460476490166911R2=0.81
RMSE=3.46
ただし、厳密に管理しようとするとまだまだ性能は甘いと思いますが今回は、学習の目的が主ですのでここでモデルの作成は完了とします。
テスト結果の可視化方法
予測した人数と実際の人数を散布図にあらわすことでおおよその当てはまり具合がみてとれます。テスト結果を散布図にしてみると、そこそこに当てはまっていますが、予想よりも実搬送人数の方が多い危険サイドよりの評価となっています。
plt.figure(figsize=(6, 4), dpi=100)
plt.scatter(pred, y_test, s = 20,marker = "o",
color = 'blue', alpha = 0.5) # 予測値と実測値の散布図
plt.xlim(0, 350)
plt.ylim(0, 350)
plt.title('予測搬送人数 vs 実搬送人数 @東京',fontsize=15) # 図のタイトル
plt.xlabel('予測搬送人数', fontsize = 15) # x軸のラベル
plt.ylabel('実搬送人数', fontsize = 15) # y軸のラベル
plt.grid(True) # グリッド線を表示
plt.tick_params(labelsize = 10)
plt.show()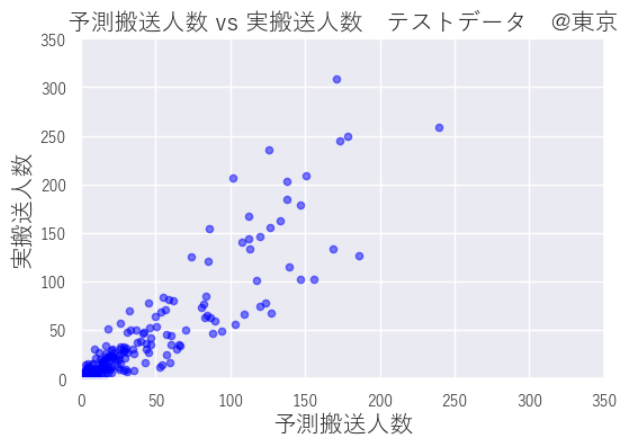
重要度の確認方法
今回のモデルのどの特徴量が影響しているのかをみていきます。feature_importanceというメソッドを使うことで、どの特徴量がどれだけ結果に影響を及ぼしたかがわかります。
結果は、やはり最も影響が大きい要素は最高気温という、まっとうな結果となりました。
df = pd.DataFrame(model1.feature_importances_, index = x.columns)
df_s = df2.sort_values(0, ascending=False)
df_s = df_s.rename(columns={0: "重要度"})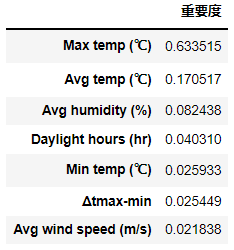
2021年5月の実際のデータでも確認してみましょう
ちなみに、直近データでも性能評価をしてみましょう。ご興味がありましたら下記からデータをダウンロードができますので実践してみてください。
東京気象データ2021年5月 ダウンロード
heatstroke003_data_r3_05 ダウンロード
# データの読み込み
df2105 = pd.read_csv("東京気象データ2021年5月.csv",encoding = "shift_jis")
# 温度差の変数を生成する
df2105[["Δtmax-min"]]=df2105["Max temp (℃)"] -df2105["Min temp (℃)"]
df2105.set_index('datetime', inplace=True) # datetimeをindexとしている
# 説明変数x_2105を生成する
x_2105 = df2105.drop(["Total precipitation (mm)"],axis=1)
# 目的変数y_2105を生成する
y_2105 = pd.read_excel("heatstroke003_data_r3_05.xlsx")
y_2105 = y_2105[y_2105["都道府県コード"]==13]
y_2105 = y_2105[["搬送人員(計)"]]
# 2021年5月の緊急搬送人数を予測する
pred2 = model1.predict(x_2105)
mae2 = mean_absolute_error(pred2, y_2105)
# RMSE 評価
import math
math.sqrt(mae2)
# RMSE:1.3323217293439518
2021年5月予測と実績の可視化
RMSEは1.33とそこそこ、グラフでみると若干バラつきが大きいような感じですね。
plt.figure(figsize=(6, 4), dpi=100)
plt.scatter(pred2, y_2105, s = 20,marker = "o",
color = 'blue', alpha = 0.5) # 予測値と実測値の散布図
plt.xlim(0, 20)
plt.ylim(0, 20)
plt.title('予測搬送人数 vs 実搬送人数 @東京 2021年5月',fontsize=15) # 図のタイトル
plt.xlabel('予測搬送人数', fontsize = 15) # x軸のラベル
plt.ylabel('実搬送人数', fontsize = 15) # y軸のラベル
plt.grid(True) # グリッド線を表示
plt.tick_params(labelsize = 10)
plt.show()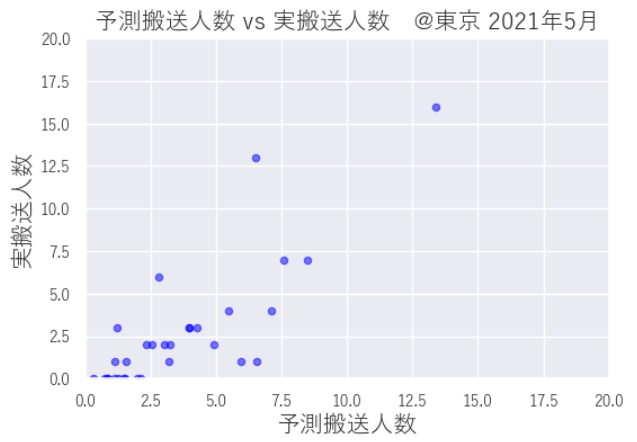
まとめ
最後まで読んでいただきありがとうございます。Pythonを使った機械学習の基本的なものはおさえられたのではないでしょうか。機械学習というとポンと答えがでてくるイメージはあるかもしれませんが、最も重要なことは記事中でもありましたが、EDA(探索的データ分析)で課題を大きく俯瞰(ふかん)して、解決策を練ることです。本記事が皆さんの業務の一助になれば幸いです。例年、梅雨明けからどんどん暑くなってきます。今回の機械学習に限らず、気温が上昇してくると当然、熱中症の危険性が高まりますので、お仕事、遊び、おうちの中でもこまめに水分をとり、お過ごしください。とくにご年配の方は、例年多くの方が発症していますのでお気をつけてくださいね。
それでは、みなさん楽しい夏を過ごしましょう!

みんな、こまめな水分、塩分補給忘れずにね

楽しい夏になるといいね♪

コメント